

Subdivision surfaces are the most common way to model complex smooth geometry in RenderMan, and for good reasons: they guarantee the smoothness of a model and they impose very few topological constraints on the modeler.
A common way to approach a subdivision surface is to imagine a polygon mesh (the control mesh) which undergoes a local averaging (or smoothing) at every vertex, creating a new set of vertices which have a smoother appearance than the original mesh. One application of this averaging operator everywhere on a mesh is a single subdivision step. If we could take an infinite number of subdivision steps, eventually we will converge to a limit surface, which has a set of guaranteed smoothness properties depending on the type of subdivision being used.
Like most other types of geometry, a subdivision mesh is described by its control mesh. Unlike NURBS, the control mesh is not confined to be rectangular, so in this respect, the control mesh is very similar to polygonal surface. But where polygonal surfaces require large numbers of points to appear smooth, a subdivision mesh's limit surface is guaranteed to be smooth - meaning that polygonal artifacts or faceting are never present, no matter how the surface animates, or how closely it is viewed.
Unlike many other renderers, RenderMan's implementation of subdivision surfaces does not apply a fixed number of subdivision steps to a polygonal mesh. Instead, it adaptively tessellates into micropolygons whose size is by default computed in term of pixels on the screen. Moreover, even if the micropolygons are large due to the micropolygon length setting, their vertices are computed directly from the limit surface for the highest accuracy.
A common question to consider when modeling assets is: should a polygonal asset be rendered as is, or should be it converted to a subdivision surface? If the asset is not smooth in nature (i.e. simple geometry with hard silhouettes), then polygons are probably all that are needed. If the asset is meant to be a smooth surface, then the tradeoffs become more complicated:
RenderMan's implementation of subdivision meshes include two subdivision schemes:
Not all geometry is smooth everywhere. In cases where a sharp feature needs to be preserved, an edge or vertex can be tagged as a crease or a corner. This means that near that feature, no actual subdivision will be applied, and the resulting limit surface will be unchanged from the control mesh.
When approximating a smooth surface with polygons, it is common to apply a fillet operator onto a sharp edge in order to convert it into a rounded edge. Unfortunately, fillets tend to create many more polygons. This problem is somewhat mitigated by conversion of the polygon mesh into a subdivision surface: now, the smoothness of the surface is guaranteed; however, the size of the rounded edge is still determined by the size of the faces adjacent to the edge, and it may still prove necessary to introduce new faces into the model to control the size of the edge curve.
To mitigate this problem, RenderMan's implementation of subdivision surfaces allow for edge and vertices to be tagged as semi-sharp creases and corners, respectively. Tagging an edge as a semi-sharp crease means that the resulting limit surface near the edge will be somewhere in between where it would have been if it had been tagged as a fully sharp crease (i.e. the control mesh) and where it would normally have ended up as a fully smooth surface. The example below shows the subdivision mesh resulting from a cube control hull, with various crease strengths applied.
A benefit of using subdivision meshes over polygon meshes is that the topological data needed to perform subdivision is also useful for guaranteeing that the surface will remain watertight, no matter what happens in the displacement. In particular, if the faces immediately adjacent to a shared edge compute a different displacement result, on a polygon mesh a crack will likely appear as the faces pull apart. While this seems like an obvious thing to avoid, in practice it may not be easy to do so particularly when using a complicated texture asset derived from PTex or a UDIM based workflow. If a subdivision mesh is used instead of a polygon mesh, with watertight dicing enabled, the renderer can ensure that no cracks will appear at face boundaries.
Watertight dicing can be significantly slower than regular dicing and lengthen the Time to First Pixel (TTFP). |
In order to provide the smoothest possible limit surface, the averaging behavior of a subdivision surface is such that the limit surface "pulls away" from the boundaries of the control mesh by default. This can be undesirable when dealing with non-closed meshes, especially those that need to connect seamlessly with other adjoining meshes. As a convenience, RenderMan provides boundary interpolation rules that allow this behavior to be overridden, allowing the surface to continue all the way to the boundary of the control mesh. Different rules allow for smooth or sharp corners (vertices which have exactly two incident edges). The example below shows the boundary interpolation rules applied to a simple 9 face control mesh.
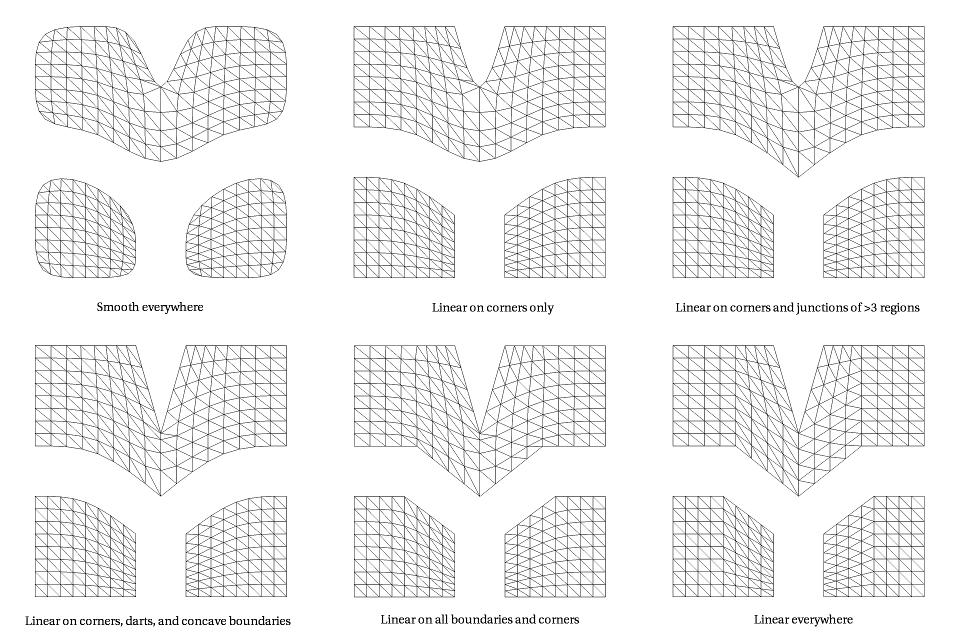
This idea of boundary interpolation can also be extended to the interpolation rules applied when dealing with data over the surface, most notably texture coordinates (in this context, RenderMan uses the term facevarying boundary interpolation). When dealing with the seams between disjoint UV regions, the renderer can use several different rules, trading off smoothness of the subdivided result away from the seams against the desire to interpolate the seams exactly. Note that no matter what rule is chosen, the UV texture map editor must also abide by the same rules, otherwise undesirable texturing artifacts will result. The following image demonstrates the different rules applied to a 4x4 grid of quads segmented into three UV regions.
The "interpolateboundary" tag controls how interpolation boundary face edges are interpolated. This tag has one optional integer argument and zero floating-point arguments. If the integer argument is not specified it is assumed to have a value of 1. A value of 0 specifies that no boundary interpolation behavior should occur (the default behavior when this tag is not specified). A value of 1 indicates that all the boundary edge-chains are sharp creases and that boundary vertices with exactly two incident edges are sharp corners. A value of 2 indicates that all the boundary edge-chains are sharp creases; boundary vertices are not affected.