In order to render images with as low noise and as fast convergence as possible, it is important to use samples that do not clump and do not leave large parts of the sampling domain empty. We call such samples well stratified.


Left: 256 random 2D samples. Right: 256 well-stratified 2D samples.
There are several different ways of generating well-stratified samples; RenderMan uses lookups in pre-generated tables of progressive multi-jittered (PMJ) sample sequences which are suitable for progressive rendering and are stratified in 1D, 2D, and 3D. The 1D sample values are between 0 and 1, the 2D samples are on the unit square, and the 3D samples are in the unit cube. (Practical tips on how to map to other domains are mentioned below.)
In order to look up in one of the pre-generated sample tables one needs to specify which table to use and which sample number is requested. RenderMan provides a convenient abstraction class and API for this, called RixRNG. The API is defined in the include/RixRNG.h header file (and the implementation of PMJ table lookups are in the include/RixRNGProgressive.h header file). The purpose of the abstraction is that authors of Bxdfs and Integrators do not have to worry about explicit indexing, sample counting, table lookups, etc.
A sample context (SampleCtx) consists of two unsigned integers: patternid and sampleid. Patternid is a 32-bit pattern that gets mapped to one of the built-in PMJ sample tables, and sampleid determines which of the samples in the table to use. Camera rays are initialized such that samples in a given pixel will have the same patternid; typically, the first sample in each pixel will have sampleid 0, the next sample in the pixel will have sampleid 1, etc.
RixRNG classThe "RNG" part of RixRNG stands for "Random Number Generator" even though the samples are not random at all. The RixRNG class is basically just a wrapper around an array of per-shading-point sample contexts (SampleCtxArray) and an integer (numPts) specifying how many sample contexts there are in the array. There is typically one SampleCtx for each point in a ray shading batch. The RixRNG wrapper class makes it convenient to generate sample points (or new sample domains) for an entire ray shading batch with just a single function call.
There are six different functions to generate samples:
GenerateSample1D()GenerateSample2D()GenerateSample3D()DrawSample1D()DrawSample2D()DrawSample3D()The GenerateSample functions increment the sample context sampleid; DrawSample functions do not.
There are also six multipoint functions that generate samples for all points in a RixRNG:
GenerateSamples1D()GenerateSamples2D()GenerateSamples3D()DrawSamples1D()DrawSamples2D()DrawSamples3D()Example: Bxdf GenerateSample() functions need 2D samples to generate sample directions. The GenerateSample() functions have a RixRNG input parameter (often called "rng") for this purpose. The RixRNG's sampleCtxArray contains numPts sample contexts, where numPts is the number of shading points to generate sample directions for. Each sample context keeps track of the patternid and sampleid for that shading point. In order to get a 2D sample for each shading point, a single call to RixRNG::DrawSamples2D() is sufficient:
RtFloat2 *xi = (RtFloat2 *) RixAlloca(sizeof(RtFloat2) * numPts); rng->DrawSamples2D(xi); // fill in xi array with numPts 2D samples |
By convention, Bxdfs call the DrawSamples1D(), DrawSamples2D(), and/or DrawSamples3D() functions. These functions do not increment the sampleids. This means that an Integrator calling a Bxdf has to do this incrementing after the Bxdf call – otherwise multiple bxdf samples will be the same sample value, ie. the same direction. Similar for light sampling and indirect illumination sampling: the Integrator has to increment the sampleids after the samples have been used. This is easily done by looping over all the sample contexts in a RixRNG like this:
for (int i = 0; i < numPts; i++)
sampleCtxArray[i].sampleid++; |
We need different sample sequences for each combination of pixel, ray depth, and domain (bxdf lobes, area lights, indirect illumination, etc.). (If the same sample sequence was used for everything, there would be correlation between samples and the image would not converge.) RenderMan internally selects sample sequences for pixel position (for anti-aliasing), lens position (for depth-of-field), and time (for motion blur), and sets up an initial patternid (bit pattern) and sampleid for camera ray hit points. All sample sequences used by Bxdfs and light source sampling need to be set up in the Integrators calling them: separate domains for bxdf, light sources, and indirect illumination derived from the parent domains – and then new domains again at the next bounce (derived from those at the first bounce), etc. This is accomplished by calling one of the NewDomain*() functions. The NewDomain*() functions create a new patternid based on a hash of the parent RixRNG's patternid and a scramble bit-pattern.
Here "domain" actually just means a different patternid bit-pattern. The name "domain" was chosen because typically a different patternid is used for bxdf sampling, light source sampling, etc., with the bxdf and light sources being different "sample domains".
First it should be mentioned that there is a special C++ type for scramble patterns. The scramble patterns are (as mentioned above) just 32-bit patterns, but these are easy to mistake for other integers. To enable the compiler to catch incorrect parameter order in various function calls, the scramble pattern has its own type – an enum class called 'Scramble' that is just an alias for unsigned int. Create a Scramble bit-pattern like this example:
RixRNG::Scramble scram = static_cast<RixRNG::Scramble>(0xfa1afe1)
There are three SampleCtx functions to generate a new SampleCtx based on an existing one, but with a different patternid: NewDomain(), NewDomainDistrib(), and NewDomainSplit().
SampleCtx NewDomain(Scramble scramble);
The simplest function is NewDomain(). Given a (32-bit unsigned int) "scramble" bit-pattern and an existing "parent" sampleCtx, it returns a new sampleCtx with a patternid that is different from the existing one (and a sampleid that is the same as the existing one). Pass a different scramble bit-pattern for different sample domains: bxdfs, light source sampling, etc. As mentioned above, the Scramble type is just an unsigned int, but made into a distinct type for type safety.
SampleCtx NewDomainDistrib(Scramble scramble, unsigned newsampleid);
The NewDomainDistrib() function is similar, but should be used where the new domain's expected number of samples differs from that of the parent and repeated visits may nor may not have the same sample count or may consume differing numbers of samples: distribution sampling. This function generates an independent sample domain where the samples in that domain are stratified with respect to each other, but not with respect to previous or future samples in the same pixel. The new patternid depends on the scramble bits, the parent's patternid, and the current sampleid – including the sampleid ensures that there is a new, independent sample distribution for every iteration. The sampleid of the new SampleCtx is set to the value of the 'newsampleid' parameter. In normal use, the new domain should be created with newsampleid = 0, and then the sampleid should be incremented every time a new sample from that domain has been used.
SampleCtx NewDomainSplit(Scramble scramble, unsigned newnumsamples);
The NewDomainSplit() function is also similar to NewDomain(), but should be used where every visit will consume the same number of samples, and it is expected that all sibling visits will also always result in the drawing of a new domain – thus exploring the full space. A fancy term for this is "trajectory splitting". (If newnumsamples is 1 this call is the same as NewDomain(scramble).)
This ensures that you will get consecutive samples from a single sample sequence, with 'newnumsamples' samples for each iteration. I.e. you will get the exact same samples values as if you had shot 'newnumsamples' as many camera rays and only 1 sample at each camera hit. In the NewDomainSplit() function, there is a line with the following: newd.sampleid *= newnumsamples. That means skipping ahead in the sequence by the splitting branching factor 'newnumsamples', thereby ensuring that the combined samples are consecutive and non-overlapping.
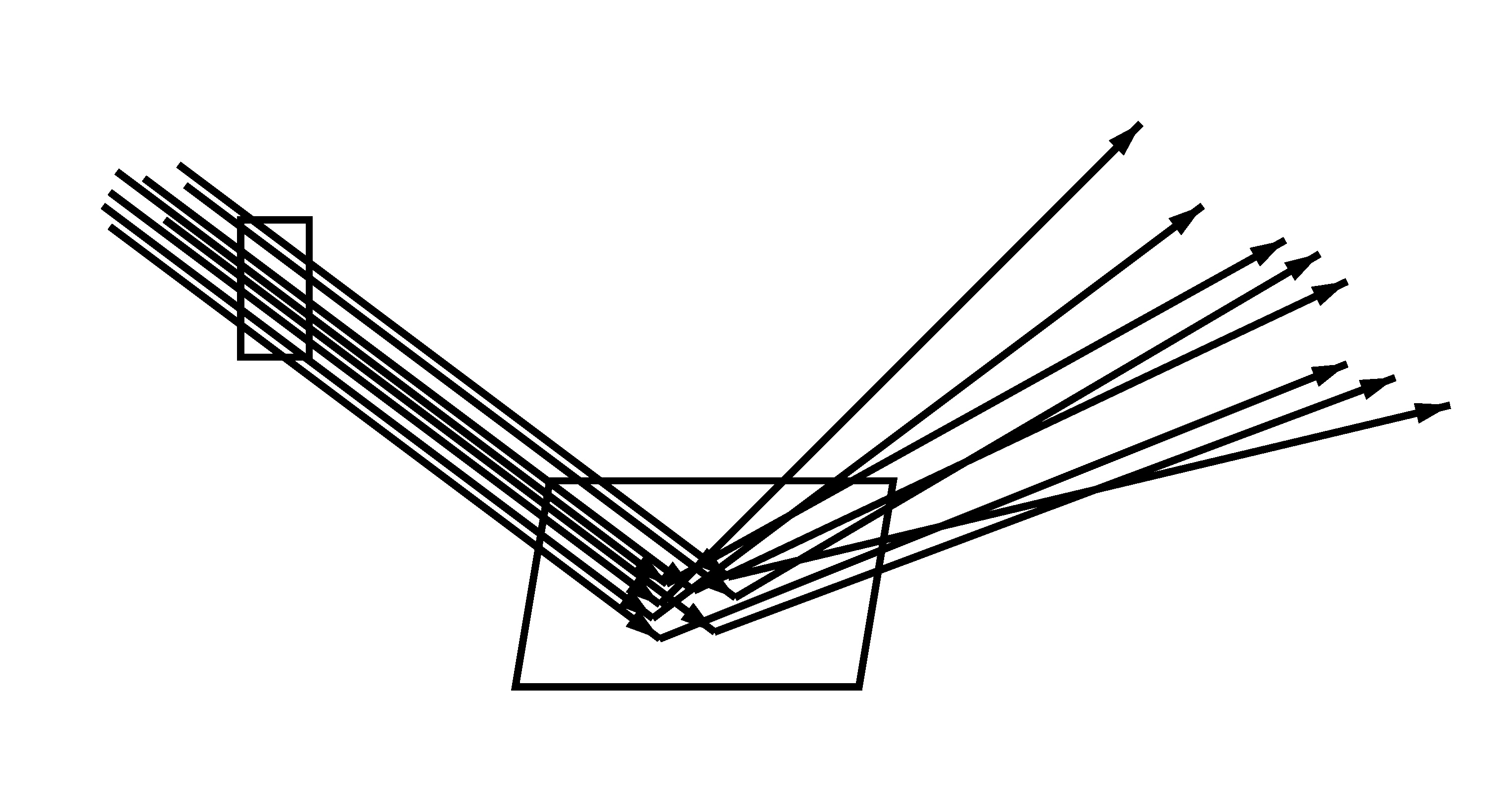
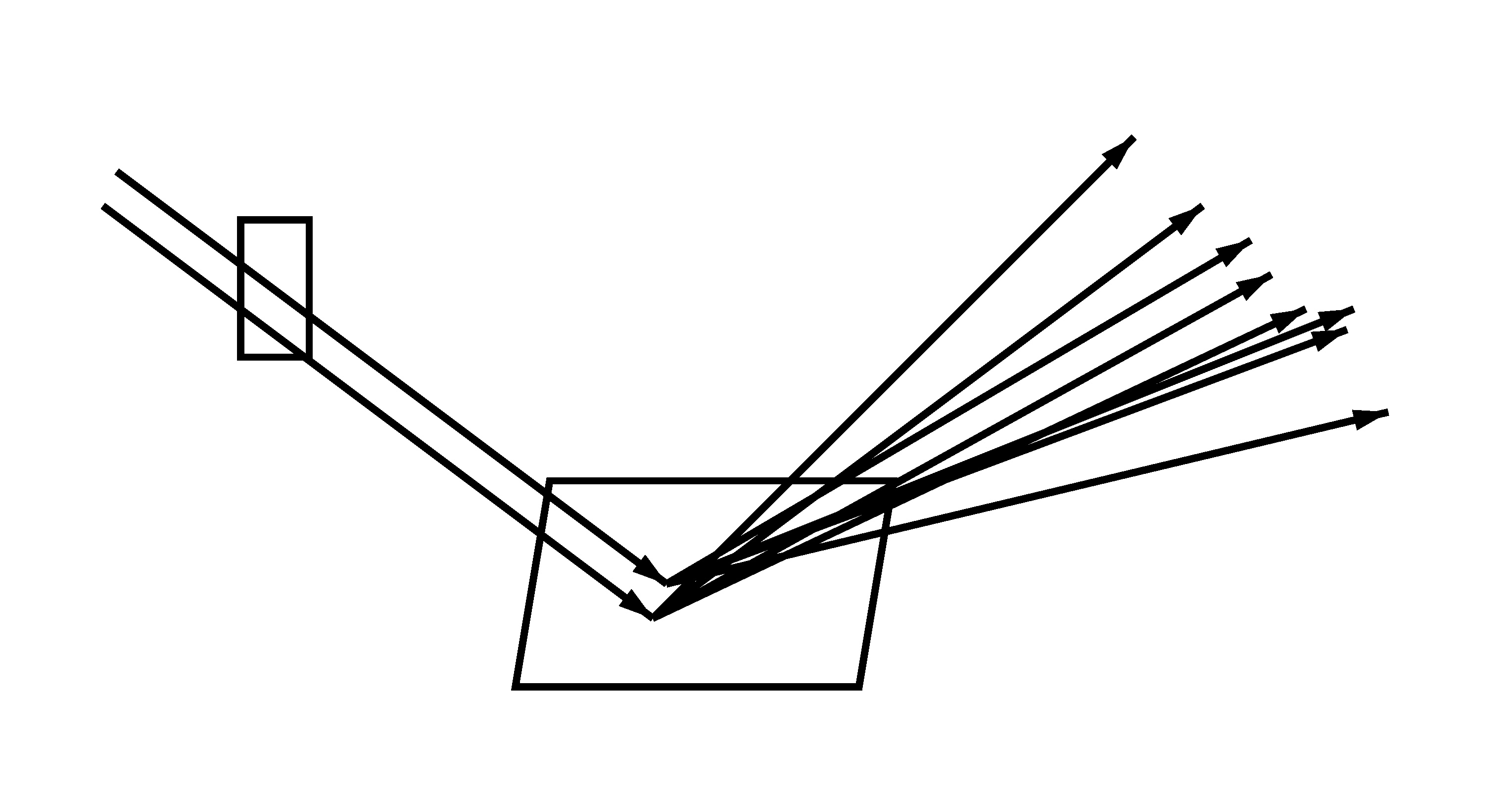
Camera rays through a pixel, hitting a surface and being reflected. Left: no trajectory splitting (8 camera rays with 1 reflection ray each). Right: trajectory splitting (2 camera rays with 4 reflection rays each). Note that the 8 reflection directions are the same in both cases.
There are also similar functions in the RixRNG class that can fill in new domains (patternids) for an entire array of sample contexts (RixRNG sampleCtxArray): NewDomains(), NewDomainsDistrib(), and NewDomainsSplit().
The scramble bit patterns can be any 32-bit pattern, but it is important that the scramble bit pattern to generate different new domains are different. For example, if an Integrator is generating new domains for bxdf and light source sampling, those should use different scramble bit patterns. Otherwise there will be correlation between bxdf and light source sampling, leading to visible artifacts and poor convergence – or even no convergence at all! Examples of bit patterns used in the PxrPathTracer Integrator are 0x2d96c92b, 0x3917fe2e, and 0xdeb189cf; there isn't anything particular about these bit patterns, the main point is that they are "random" and different. The same scramble bit patterns can be used at different ray depths because the parent ray's patternids will differ, so when we generate a new patternid based on a different parent patternid and the same scramble, the new patternid will be different.
Integrators call RixRNG constructors to set up sample domains for bxdfs lobe selection and sampling, light selection and sampling, stochastic transmission, volume scattering, and several other things.
There are several different RixRNG constructors. The simplest ones are simply passed an already allocated sample context array and its size, and assigns these to the RixRNG sampleCtxArray and numPts member variables. The data in the sampleCtxArray (patternids and sampleids) can be filled in before or after the RixRNG constructor call. The more fancy RixRNG constructors construct a new RixRNG based on an existing one and fills in all the sampleCtxArray values – optionally with splitting or distribution. These fancy constructors are convenient when the number (and order) of shading points in the new RixRNG matches the shading points in the parent RNG. If the number (or order) is different, then the sample contexts in the new RixRNG has to be initialized individually – as in the following example.
Example: Here is an example where a sampleCtxArray is allocated, a RixRNG is constructed (containing that sampleCtxArray), and the RixRNG's sampleCtxArray is initialized by by looping over shading points:
SampleCtx* samplectxarray = new SampleCtx[numPts];
RixRNG rng(parentRng, samplectxarray, numPts);
RixRNG::Scramble scramble = static_cast<RixRNG::Scramble>(0x8732f9a1)
for (int pt = 0; pt < numPts; pt++)
{
int index = shadingContext->integratorCtxIndex[pt];
samplectxarray[pt] = parentRng→NewDomainSplit(index, scramble, 4);
} |
Here the scramble bit-pattern is 0x8732f9a1 and the splitting factor is 4.
This section contains a few practical tips for how to use the samples returned by the RixRNG DrawSample* and GenerateSample* API functions.
The samples returned by the DrawSample2D() and GenerateSamples2D() functions are in the unit square. It is often necessary to map from the unit square to other domains. Example: uniform sampling a disk with a given radius can be done by picking a radius proportional to the square root of a sample between 0 and 1, and an angle between 0 and 2pi, and then computing the xy position corresponding to that radius and angle:
RtFloat2 sample = rng->DrawSample2D(i); float r = radius * sqrt(sample.x); float angle = 2 * M_PI * sample.y; point.x = r * cos(angle); point.y = r * sin(angle); |
An arguably better mapping from the unit square to a disk is Shirley and Chu's concentric mapping. (See Pete Shirley's blog for the most efficient implementation.)
Other common mappings map samples to the surface of a sphere, hemisphere, or cylinder, map samples to directions proportional to a glossy bxdf lobe, and so on.
We often need to combine a selection between sub-domains and generation of positions (or directions) on one of those sub-domains. For example: select a light source and generate a sample position on that light source, or select a bxdf lobe and generate a sample direction proportional to that lobe.
One way to do that is to get a 3D sample and use the z coordinate to choose the sub-domain, and the xy coordinates to select the position (or direction) in that sub-domain. This can be a fine way to do this when the samples are well stratified in 3D and their xy coordinates are well stratified in 2D.
A common – equally good – alternative is called "Shirley remapping". It does not rely on 3D stratification, but only on 2D stratification. Get a 2D sample and first use one of the coordinates of the sample to select the sub-domain, and then map the samples within that selected domain (based on the selection probability) back to the unit square domain. A figure provides a more intuitive explanation – in this example we choose between two light area sources, with 80% chance of selecting the first light and 20% chance of selecting the second light:



To the left are the original samples on the unit square. The middle square contains the samples from the left 80% of the original samples, only stretched a bit horizontally. Likewise, the right square contains the samples from the right 20% of the original samples, but stretched 5x horizontally. The stretching preserves the stratification properties of the original sample points.
This method of using 2D samples to both choose between sample sub-domains and at the same time stretching the samples from the chosen sub-domain to provide stratified 2D sample points is implemented in the RixChooseAndRemap() function in the RixShadingUtils.h include file.
Path splitting and distribution ray tracing were mentioned above (in the description of the various NewDomain*() functions). But when is it appropriate to use which? A couple examples should provide some guidance:
Use path splitting if there is a known, fixed branching factor. For example, if all camera ray hits spawn four direct illumination rays then NewDomainSplit() can correctly offset into the sample sequence so that all samples in the sequence are used exactly once. This way, the direct illumination ray directions from all camera ray hit points for a given pixel combine into one well stratified sample pattern.
Resort to distribution ray tracing if there is no fixed branching factor. For example, if some specular ray hit points spawn 16 new sample directions but other specular ray hit points (perhaps with a lower throughput) only spawn 4 or even 1 new sample directions. In this case there is no simple way to compute the offset into a combined sample sequence. Instead the 16 (or 4) sample directions are stratified with respect to each other, but not with respect to any other samples for that same pixel. (If only 1 new sample direction is spawned then there is no stratification at all.)
Non-stratified samples similar to e.g. drand48() can be obtained by calling the HashToRandom() function. It computes a repeatable random float between 0 and 1 given two unsigned int inputs, for example patternid and sampleid. Using the same patternid and continuously incrementing sampleid gives a sequence of samples with good statistical variation – similar to drand48(). The HashToRandom() function is repeatable (i.e. the same two inputs always give the same output), and has no multi-threaded contention (whereas drand48() has notoriously bad cache line contention, hampering multi-threaded performance). HashToRandom() is located in the RixRNGInline.h include file.
In the introduction above we wrote that patternid is used to choose the PMJ table, and sampleid is used to choose the sample in that table. If we had 2^32 pre-generated PMJ tables it really would be as simple as that. However, in practice we have only 384 different PMJ tables, so we have to be a bit inventive to make it look like we have many, many different tables even though we don't. The trick – implemented in include/RixRNGProgressive.h – is to further "randomize" the samples in the tables. This randomization is done with scrambling of the sample values and shuffling of the sample order. First the patternid is mapped to one of the 384 PMJ tables with a repeatable hash function. Then the sampleid is shuffled a bit by carefully swapping neighbor samples and groups of four samples. (Such local shuffling does not affect the convergence properties of each sample sequence, but decorrelates sample sequences such that they can be safely combined with each other.) Finally the mantissa bits of the floating-point sample values are scrambled using the patternid – this scrambling changes the sample values while preserving their stratification.
Another practical detail is that even though PMJ sequences theoretically have infinitely many samples, in practice we limit each PMJ table to 4096 samples to keep memory use reasonable. When more than 4096 samples per pixel are used – i.e. sampleid values higher than 4096 – we look up from the beginning of another PMJ table (also with 4096 samples). So the samples beyond 4096 are still stratified, just not quite as well stratified with respect to the first 4096 samples as if we had had larger tables. For more than 8188 samples per pixel we move to yet another table, and so on. In the unlikely case that more than 196608 samples per pixel are used, we run out of tables – in this case the samples revert to unstratified, uniform (but deterministic) pseudorandom samples generated with the HashToRandom() function described above.
It is possible to override the default PMJ samples if other sample sequences are desired. This is scary stuff, but can be useful for experimenting with e.g. primary-space Metropolis rendering algorithms or adaptive progressive photon mapping. The Generator class provides a way to intercept sample generation: when a custom Generator has been specified, it automatically gets called when e.g. a Bxdf or light sampling calls one of the GenerateSample*() or DrawSample*() functions. Some of the RixRNG constructors can be passed an explicit pointer to a Generator.
For example, for debugging purposes it can be useful to have all samples generated by drand48(). (Note that drand48() is very bad for regular use: convergence is slow since its values are not stratified, and it has cache line contention for access to its internal state, which slows down multi-threaded executions.) Here is a snippet of code from a Generator that calls drand48():
class RandomSampler : public RixRNG::Generator
{
...
// Generate a uniformly distributed pseudorandom sample in [0,1)
virtual float Sample1D(const RixRNG::SampleCtx &sc, unsigned i) const // both params are ignored
{
float x = drand48();
if (x >= 1.0f) x -= 1.0f; // this can happen due to rounding double to float
return x;
}
... similar Sample2D() and Sample3D() functions ...
// Fill in float array 'xis' with pseudorandom samples in [0,1)
virtual void MultiSample1D(unsigned n, const RixRNG::SampleCtx &sc, float *xis) const
{
for (int i = 0; i < n; i++)
{
float x = drand48();
if (x >= 1.0f) x -= 1.0f; // this can happen due to rounding double to float
xis[i] = x;
}
}
... similar MultiSample2D() and MultiSample3D() functions ...
} |
For more (very nerdy!) details about the properties of PMJ samples please refer to the following paper:
"Progressive multi-jittered sample sequences",
Per Christensen, Andrew Kensler, and Charlie Kilpatrick,
Computer Graphics Forum (Proceedings of the Eurographics Symposium on Rendering), 37(4):21-33, 2018.
Paper and presentation slides are available here: graphics.pixar.com/library/ProgressiveMultijitteredSampling